Finance 101
Let’s start with a simple question:
“Ajay is interested to avail a sum of 10000$ from a bank for his equity investments, he is given 2
options- he can avail the loan today or on the same day ,1 year from now.”
What would you suggest to Ajay? This question requires the understanding of ‘Time Value of money’.
YES, this is because the value of money changes with time.
Time Value of Money (TVM)
Definition:
Money available at the present time is worth more than the same amount in the future due to its
potential earning capacity. The founding principles of finance state that if money could earn interest,
then the same amount of money is worth more the sooner it is received.
Formula

Illustration
Q. If you wish to accumulate $140,000 in 13 years, how much must you deposit today in an account that pays an annual interest rate of 14%?
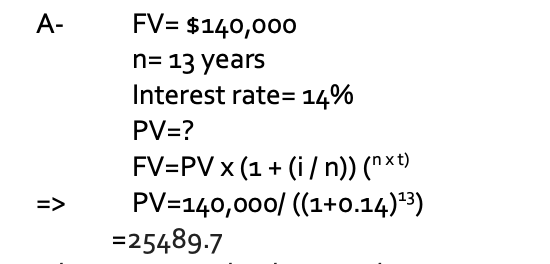
The amount to be deposited =$25490
To understand this concept more clearly and how this works, let us introduce the following terms:
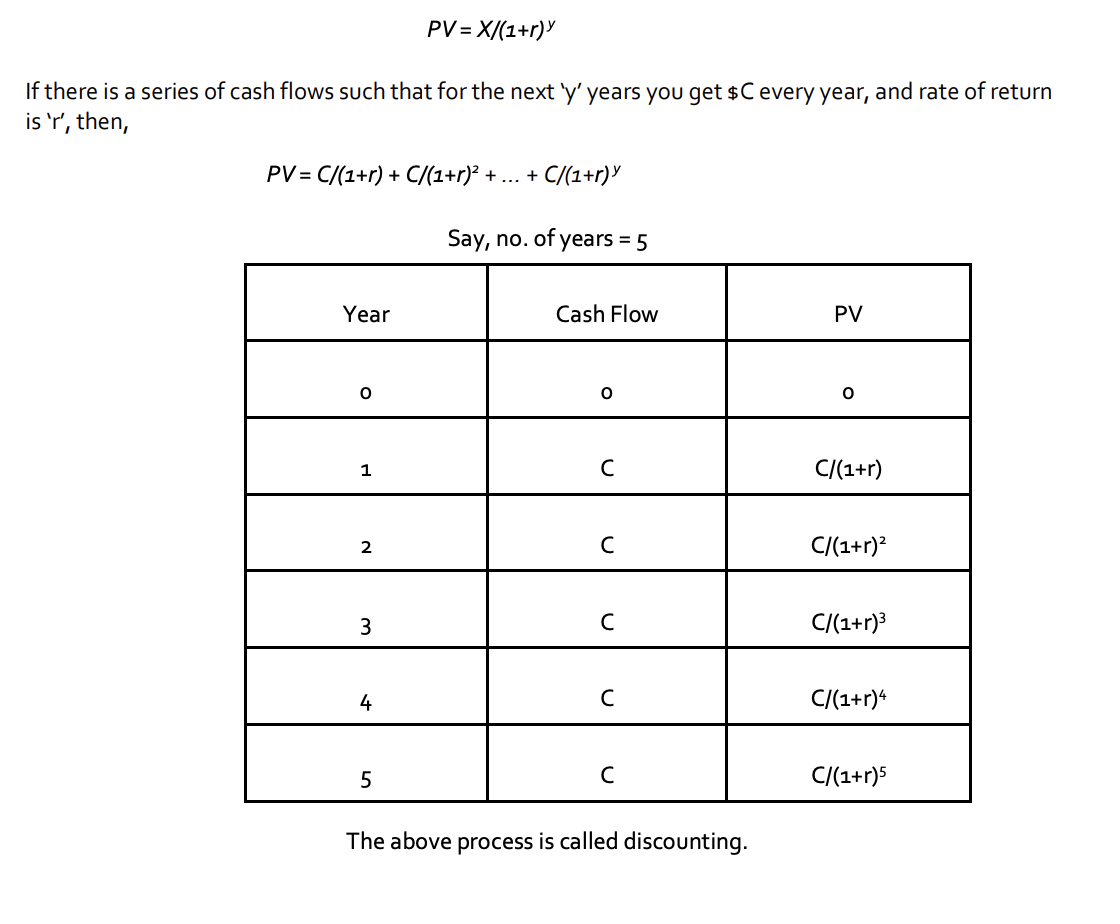
PRESENT VALUE(PV)
Definition:
It is the current value/worth of a future sum of money or a series of cash flows for a given rate of return.
For example, an amount of $1000 in the year 2030 will be less valuable than $1000 today.
Formula
Suppose ‘$X’ is the amount of money you have ‘y’ years from now, and the rate of return is ‘r’. Then,
FUTURE VALUE(FV)
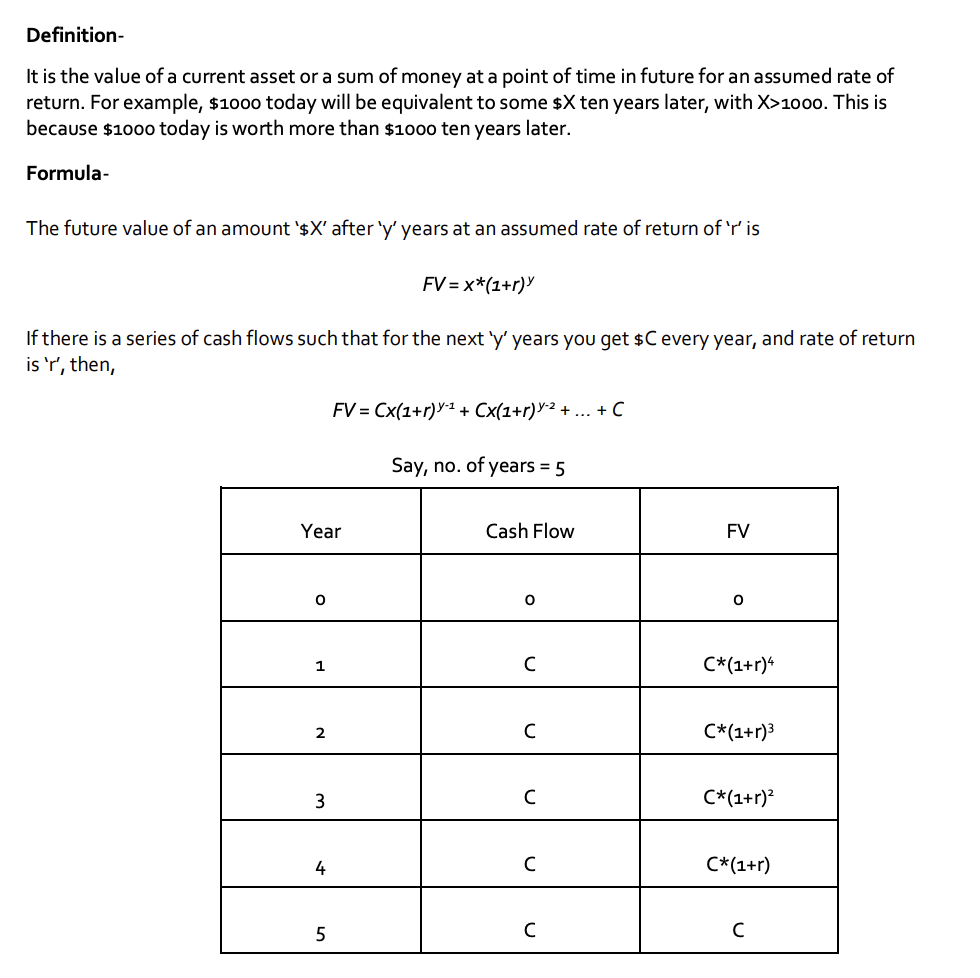
For finding both PV and FV, the fundamental concept involved is that of compounding. Also note, the rate of return(r) is determined by the market. No individual can control the value of r.
Suggested Video
https://www.investopedia.com/terms/f/futurevalue.asp
Illustration
Q. What should be the cost of a car which costs $100000 today, four years from now? Assume that the rate of return is 10% per annum.
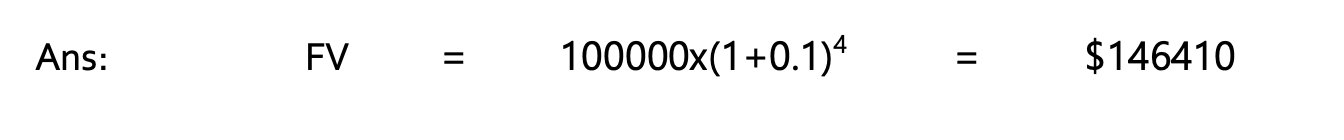
Q. Calculate the present value of a series of cash flows, which gives you $500 a year for the next 10 years. Assume the rate of return/discount to be 5%.

ANNUITY AND PERPETUITY
Definition:
An annuity is a continuous cash flow scheme, where you receive a fixed amount of money at certain intervals (generally a year) for a certain number of time periods. In a perpetuity, there is no termination of the scheme, and you continue receiving the amounts ad infinitum.
Formula:

The formulas are explained in the next section.
The Maths Behind It
The table below shows the cash flow coming in at each interval, and the corresponding present value of
the amount.
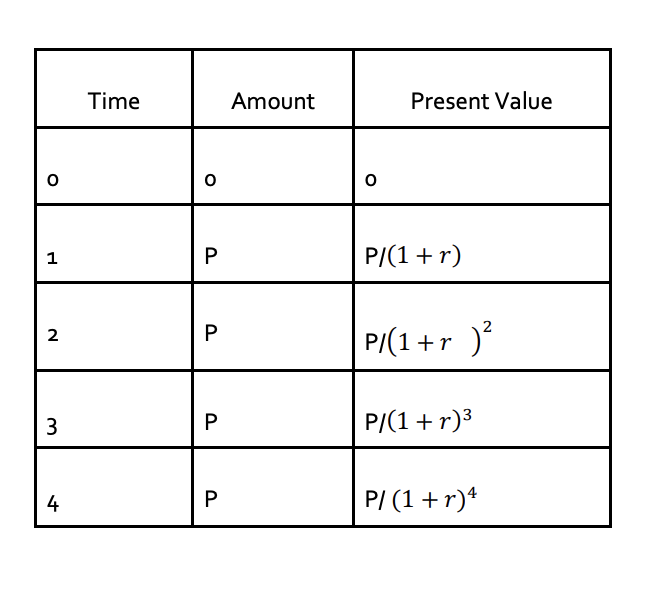
Similarly, summing the terms, which are in a Geometric progression, we get the general formula for the
PV of an annuity.
In case of a perpetuity, it is an infinite Geometric Progression with common ratio 1/(1+r).
Therefore, we can find the sum accordingly as,
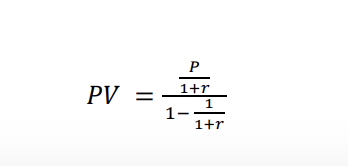
NOTE - The above formula must be making you think how an infinite stream of cash flows has a finite fixed value. This is because, the real values of the cash flows keep decreasing every time. As time passes, due to inflation, the real values keep decreasing. As the time tends to infinity, the total sum converges, since the real values of the cash flow tend to zero.
Interpretation and Usage
Annuities are the schemes used for post-retirement fixed income, which ensures a fixed amount
received every month. Also, EMIs(Easy Monthly Installments) are also a form of annuities, where the
amount to be paid is arrived at by calculating the PV of the annuity.
An example of a perpetuity is the British govt-issued CONSOL bonds. Herein, the bondholder receives
fixed coupon payments periodically as long as the government does not discontinue the consol.
One point to be noted is, if the interest rate of an annuity is lesser than the inflation rate, you might be
in for a loss, and such an investment is unadvisable.
Exercise
1. Calculate the present value on Jan 1, 2017 of an annuity of Rs. 500 paid at the end of each
month of the calendar year 2017. The annual interest rate is 12%.
A. Rs. 5627.54
2. A certain amount was invested on Jan 1, 2010 such that it generated a periodic payment of
$1,000 at the beginning of each month of the calendar year 2010. The interest rate on the
investment was 13.2%. Calculate the original investment and the interest earned.
A. Rs. 692.68
NET PRESENT VALUE(NPV)
Definition:
The net present value is the difference between the investments and cash flows, all discounted to the
present time.
Formula
Suppose in a project initial investment is I, the resulting cash flows at the end of year be C1, C2,
C3…..Cn. The discount rate is r. These cash flows can be positive (in case of income) and negative (in
case of expenditure)
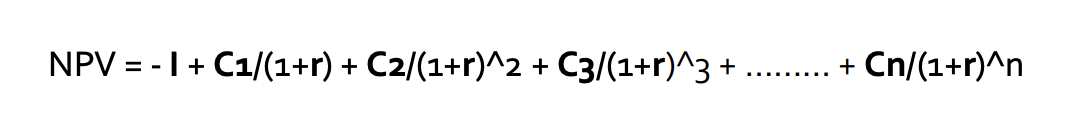
Interpretation and Usage-
NPV can be used to make a comparison between projects.
- Positive NPV: Profitable Project
- Negative NPV: Net loss
How is it different from PV?
NPV is the net summation of all PV. In PV we assumed that the discount rate is constant but we can vary the discount rate r in case of NPV also, in case of PV we assume that the capital expense happened in year 0 and all cash flows henceforth are positive while in case of NPV we can account for both positive and negative cash flows throughout the investment period.
Excercise:
Martin started a business at the start of year 2005. He invested 200$ in the beginning. The expected
cash flows at the beginning of subsequent years are 50$ and 60$. Forecasting the recession in the year
2008 he assumed a loss of 20$. (All cash flows at the beginning of year). Calculate the net present value
of the project in the year 2005 assuming a constant interest rate of 10%.
Ans. 120$
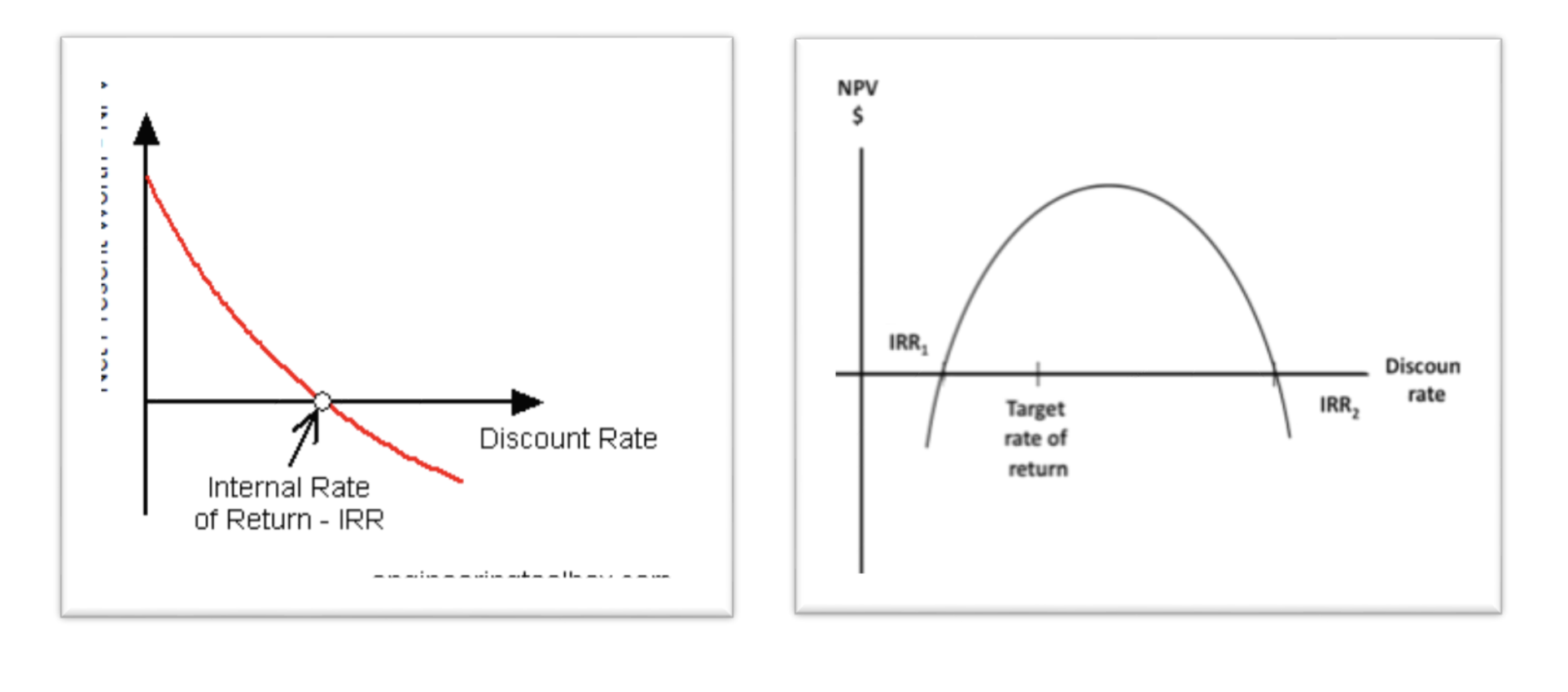
INTERNAL RATE OF RETURN (IRR)
Definition:
A discount rate that makes the net present value (NPV) of all cash flows from a particular project equal
to zero.
Formula
Suppose in a project initial investment is I, the resulting cash flows at the end of year be C1, C2,
C3…..Cn.
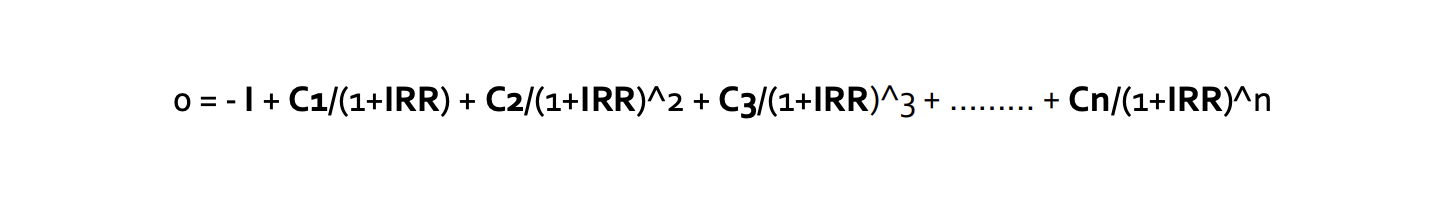
Interpretation and Usage-
IRR can be used to compare the profitability between projects. The project with higher IRR is considered better. IRR should at least exceed the considered cost of capital.
Excercise
Martin started a business at the start of year 2005. He invested 80$ in the beginning. The expected cash
flows at the beginning of subsequent years are 50$ and 60$. Forecasting the recession in the year 2008
he assumed a loss of 20$. (All cash flows at the beginning of year). Calculate the IRR of the project.
Ans. 10%
Misleading Nature:
- A project can have multiple IRR, the number of IRR equals to the number of times the sign of cash flows changes.
- IRR is biased and is favored to that project for which initial cash flow are more. So, it is biased to short term projects which have low investments.
- Does IRR even make sense?
“MAYBE” It is deceptive.
Suggested Video
http://www.investopedia.com/terms/i/irr.asp
