Game Theory

Basic Terminology

Game
Any situation / set of circumstances which has two or more decision makers(players) involved, where the result is dependent on the actions of all the decision makers.

Player
A participant in a game, whose decisions influence what benefit he derives from the game. The aim of the player is to maximize that benefit.

Strategy
A strategy is a plan of action, which a player in a game may pursue / plan to pursue, depending on the circumstances under which the game is being played. Strategy may change over the course of the game.

Payoff
A numerical value which estimates the relative/absolute benefit a player may get from a particular outcome of a game. The payoff is quantifiable in some cases, like money or number, but in other cases, it can be evaluated on utility.

Information set
An information set is the total information available to the player in a game at any instant in the duration of the game. The information set is mostly used when sequential games are involved.

Equilibrium
Equilibrium is reached in a game when all players have made their decisions, and an outcome has come into effect.

Assumptions

There are numerous factors influencing the decisions and outcome of a game. The more the factors, the harder it becomes to predict the course of play, and the effect of factors. Thus, we assume a few things in order to proceed to analyze the situations.

1. We assume that, in a game, all players behave rationally. This means they take all decisions based on the available information, past history and a rational outlook. In the real world, though, people often become illogical and take brash decisions.
2. It is assumed that every player in a game wants the maximum payoff available, and this will influence his decisions to a great extent.
3. Game theory assumes, and expects, games to be completely descriptive. This means, all possible outcomes are defined and covered, and payoffs for each player are defined for each outcome. The description is supposed to answer all “what if”s .

Types of Games

• Cooperative /non cooperative
  

  A game is cooperative if the players are able to form binding commitments externally enforced (e.g. through contract law). A game is non-cooperative if players cannot form alliances or if all agreements need to be self-enforcing

• Symmetric /asymmetric
  

  A symmetric game is a game where the payoffs for playing a particular strategy depend only on the other strategies employed, not on who is playing them. If the identities of the players can be changed without changing the payoff to the strategies, then a game is symmetric. The standard representations of chicken, the prisoner's dilemma, and the stag hunt are all symmetric games.

• Zero-sum / Non-zero-sum game
  

  Zero-sum games are a special case of constant-sum games, in which choices by players can neither increase nor decrease the available resources. In zero-sum games the total benefit to all players in the game, for every combination of strategies, always adds to zero. Poker is one of the best examples of zero sum games. Non-zero-sum games may turn out to be a bit beneficial for all parties.

• Simultaneous / Sequential
  

  Simultaneous games are games where both players move simultaneously, or if they do not move simultaneously, the later players are unaware of the earlier players' actions (making them effectively simultaneous). Sequential games (or dynamic games) are games where later players have some knowledge about earlier actions.

Sequential Games

In game theory, a sequential game is a game where one player chooses their action before the others choose theirs. Importantly, the later players must have some information of the first choice, otherwise the difference in time would have no strategic effect. Sequential games hence are governed by the time axis, and represented in the form of decision trees.

A common way of representing games, especially sequential games, is the extensive form representation, which uses GAME TREES. Game trees are made up of nodes and branches, which are used to represent the sequence of moves and the available actions, respectively.

Consider two players, Mr Black and Ms White, who are playing a sequential game. Mr Black moves first and has the option of Up or Down. Ms White then observes his action. Regardless of what Mr Black chooses, she then has the option of High or Low.

The game tree for this game would appear as follows:

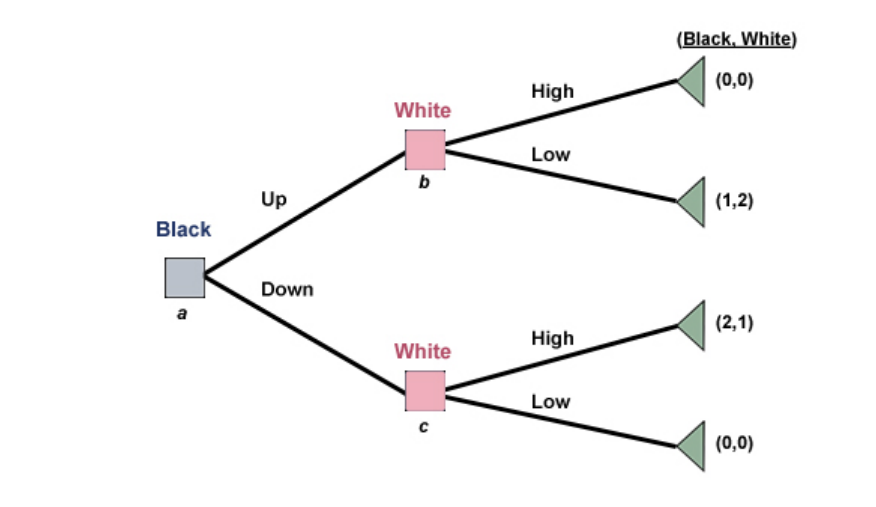
Node a is the decision node where Mr Black chooses between Up and Down. Since node a is the first node, it is also known as the initial node. Nodes b and c are the decision nodes at which Ms White chooses between High and Low. The ending nodes on the right are the terminal nodes, which also have the payoffs for each player associated with each outcome listed beside them.

BACKWARD INDUCTION
In this process, the game tree is essentially flipped. Working backwards from the payoff, the decision-maker begins to eliminate suboptimal actions until only the most likely path remains. By doing this, an opponent's likely moves from the initial node to the payoff can be mapped, allowing the decision-maker to strategize for each of those potential moves and ultimately find equilibrium.

REPEATED GAMES
In game theory, a repeated game is an extensive form game that consists of a number of repetitions of some base game (called a stage game). The stage game is usually one of the well-studied 2- person games. Repeated games capture the idea that a player will have to take into account the impact of his or her current action on the future actions of other players; this impact is sometimes called his or her reputation. Single stage game or single shot game are names for non-repeated games.

INFINITELY REPEATED GAMES
Games that are repeated infinite number of times. It is found that the preferred strategy is not to play a Nash strategy of the stage game, but to cooperate and play a socially optimum strategy. An essential part of strategies in infinitely repeated game is punishing players who deviate from this cooperative strategy. The punishment may be playing a strategy which leads to reduced payoff to both players for the rest of the game (called a trigger strategy). A player may normally choose to act selfishly to increase their own reward rather than play the socially optimum strategy. However, if it is known that the other player is following a trigger strategy, then the player expects to receive reduced payoffs in the future if they deviate at this stage. An effective trigger strategy ensures that cooperating has more utility to the player than acting selfishly now and facing the other player’s punishment in the future.

FINITELY REPEATED GAMES Games that are repeated finite number of times or games whose time period is known. It is optimal to play the Nash strategy of the stage game in all periods. When the Nash equilibrium payoff is equal to the minmax payoff, then the player has no reason to stick to a socially optimum strategy and is free to play a selfish strategy throughout, since the punishment cannot affect him (being equal to the minmax payoff)

Simultaneous Games
A simultaneous game is where all the players choose the action to pursue without any knowledge of the actions taken by the other player. A simple and familiar example of this would be the game of rock, paper, scissors. Here, the players play their move without knowing what the other player is playing. To analyse the situation and come up with the suitable plan of action we create something called the ‘playoff matrix’. This matrix lists down all the actions a player can make and the respective payoff, or in other words, a numerical value denoting how well off (or worse off) the player would become.

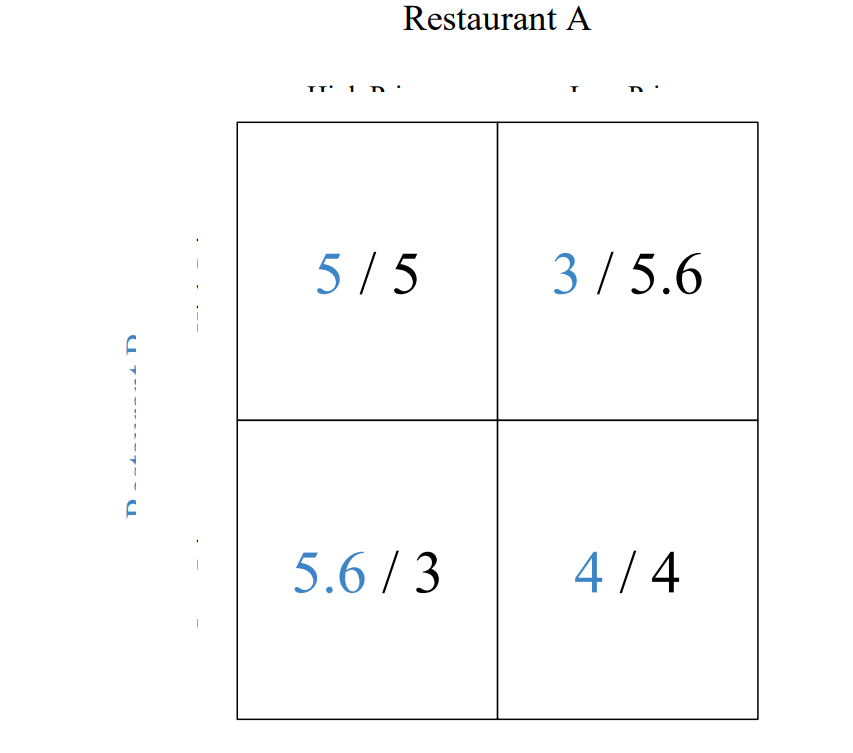
Let us consider the case of 2 restaurants. They have the choice of setting their prices high or low, i.e., 100 or 80 rupees respectively. There are about 10,000 customers out of which 3,000 prefer one restaurant and 3,000 others prefer the other restaurant. This means that they will eat at their preferred restaurant no matter what the price is. The other 4,000 customers are price sensitive, choosing the cheaper restaurant. Let us say that both the restaurants set a high price. Then, 5,000 customers would eat at each restaurant earning them a revenue of 5,00,000. If both set a low price they earn a revenue of 4,00,000. If one sets a high price then they earn revenues of 3,00,000 and the other restaurant earns 5,60,000. The payoff matrix would look like this:

Once we know the different strategies that the other player can use we can come up with our own strategy. Let us continue with our restaurant's example. Let us assume restaurant A prices their food at 100. Then, restaurant B would make more revenue by charging lower prices, 5.6 lakhs compared to 5 lakhs. Next, let’s assume restaurant A charges the lower prices. Then too, it makes more sense for restaurant B to charge lower prices since that would allow them to earn 4 lakhs compared to the 3 lakhs from charging higher prices.

In this case, as we can see, it makes more sense for Restaurant B to charge low prices as they would be better off in both scenarios, Restaurant A charging a higher price or charging a lower price. Such a strategy is called the dominant strategy. A dominant strategy always does better than any other strategy the player can adopt, regardless of what the other players in the games plan on doing. In our example, for Restaurant B charging lower prices in the dominant strategy as they would also do better by doing this than charging higher prices.

Similar to the dominant strategy we have the dominated strategy. This strategy always does the

worse than other strategies no matter what strategy the other player adopts. In our example, setting a high price is the dominated example.

As we have seen, it would make sense for Restaurant B to charge a lower price. Similarly, by symmetry, it would make more sense for Restaurant A to charge lower prices as well. Hence, both restaurants would charge a lower price. This is our Nash Equilibrium. This equilibrium is the strategies played by the different players such no player would have an incentive to change their strategy. Changing their strategies would only make them worse off.

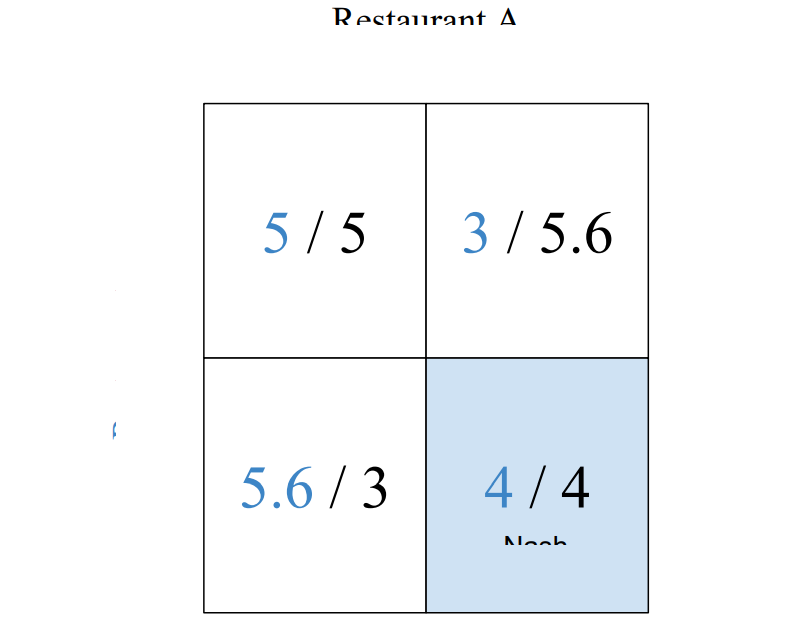
In our example we observed a single Nash Equilibrium. However, there may be multiple Nash Equilibria in a game